Research interests
Most of my research is on geometrical problems that arise from the study of surfaces. Below I explain some of my projects.
Most of my research is on geometrical problems that arise from the study of surfaces. Below I explain some of my projects.
|
|
|
|
Square-tiled surfaces
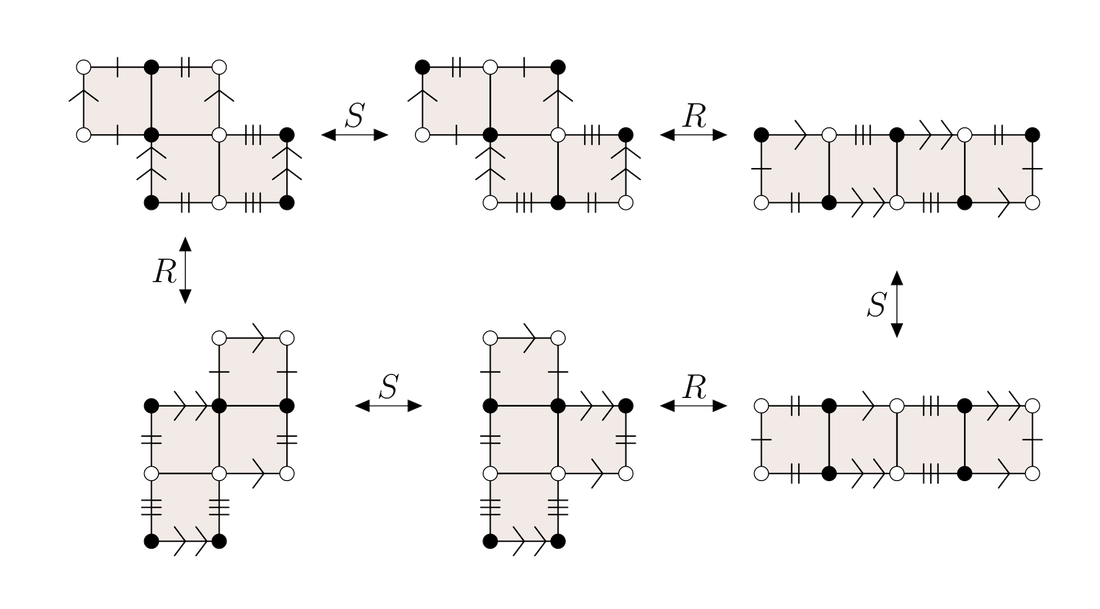
A square-tiled surface is a collection of unit squares in the plane whose pairs of parallel sides are identified by translations. One can think about them as geometric tilings on topological surfaces. The simplest example of a square-tiled surface is a single unit square with opposite sides identified. Topologically it is a torus, geometrically it has a flat (or Euclidean) metric with an extra symmetry given by rotation by 90 degrees, algebraically it is an elliptic curve with j=1728. It also can be thought of as a quotient of the complex plane by an integer lattice. The group SL(2,Z) acts on the complex plane and preserves the lattice, therefore it preserves the square torus. Lifting this action, one obtains the action of SL(2,Z) on the set of all square-tiled surfaces. There is a problem of classification of square-tiled surfaces up to this action. In my thesis I am giving a partial answer to this problem in genus 2. |
|
Spaces of branched covers
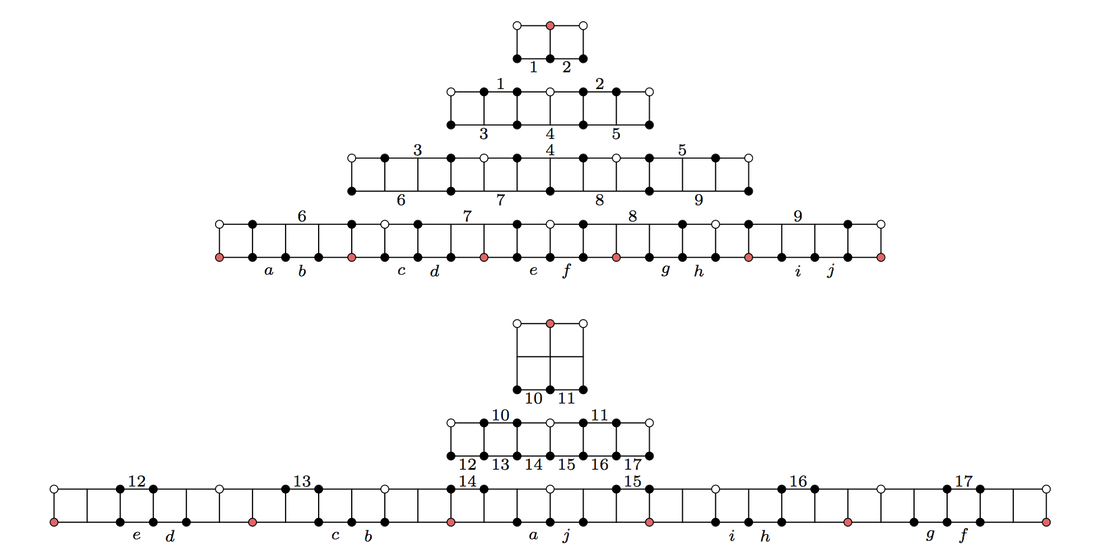
I study the geometry of the parameter spaces of branched covers of a torus, or absolute period leaves. Surfaces of genus 2 that cover the square torus have at most two branch points and the relative position of these points on the square serves as a coordinate on the absolute period leaf. It's turns out that in this case the absolute period leaf is itself a surface with a square-tiled structure. Such absolute period leaf exists for any degree of the cover. In my thesis I describe the geometry of the absolute period leaves for prime degrees and show that interesting structures, called pagodas, arise in this case. These structures are closely related to the problem of classification of square-tiled surfaces. |
|
Surfaces with many symmetries
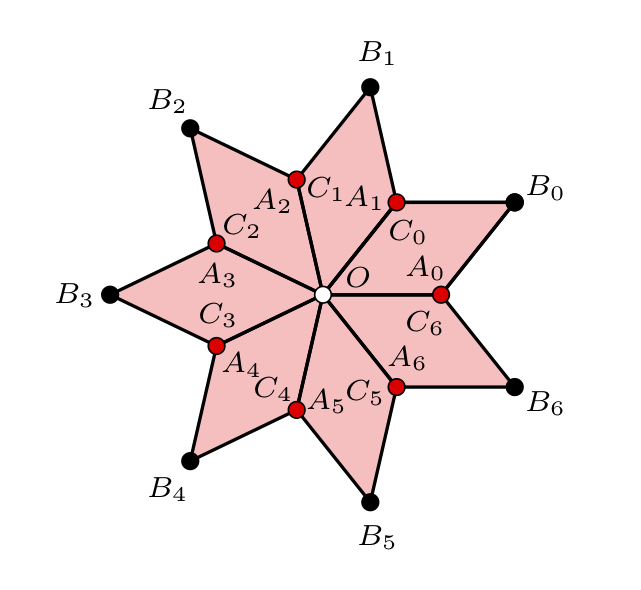
A 1-form on an algebraic curve (alternatively, Riemann surface) can be used to unfold the curve into Euclidean plane via integration obtaining a translation surface, a collection of polygons with pairs of parallel equal sides identified by translations. However, in general, given a translation surface it is impossible to identify the underlying algebraic curve. Fortunately, some algebraic curves have exceptionally many automorphisms, or symmetries: they don't come in continuous families of surfaces with the same group of automorphisms. In joint project with Leonid Monin we exploit this property to construct translation surfaces supported on such algebraic curves. In other words, an induced action of an automorphism on the space of holomorphic 1-forms on the curve has an eigenbasis. We present such eigenbases for three infinite series of algebraic curves as translation surfaces and explore the connections between flat metric and algebro-geometric properties of such curves, such as the Jacobian. |